14.1 Beta-binomial

Prior

  • \(p \sim Beta(\alpha, \beta)\)
  • \(E[p] = \frac{\alpha}{\alpha + \beta}\)
  • \(Var[p] = \frac{\alpha\beta}{(\alpha+\beta)^2 (\alpha + \beta + 1)}\)

Data: y, n

Posterior - \(E[p|y] = \frac{\alpha + y}{\alpha + \beta + n}\) - \(Var[p|y] = \frac{(\alpha+y)(\beta+n-y}{(\alpha+\beta+n)^2 (\alpha + \beta + n + 1)}\)

Posterior alpha and beta for plotting the posterior distribution from https://en.wikipedia.org/wiki/Beta_distribution#Mean_and_variance

  • \(\nu = \frac{\mu(1-\mu)}{\sigma^2} - 1\)
  • \(\alpha = \mu\nu = \mu\Big(\frac{\mu(1-\mu)}{\sigma^2} - 1\Big)\)
  • \(\beta = (1-\mu)\nu = (1-\mu)\Big(\frac{\mu(1-\mu)}{\sigma^2} - 1\Big)\)

Example code

Code 
alpha = 2   
beta  = 2   

mu = alpha*beta
sigma2 = alpha*beta/((alpha+beta)^2*(alpha + beta + 1))

## suppose y successes in n trials games
y = 10
n = 10

## Posterior mean and variance
post.mu = 
  (alpha + y)/
  (alpha + beta + n)

post.sigma2 = 
  (alpha + y)*(beta + n - y)/
  ((alpha + beta + n)^2*(alpha + beta + n + 1))

## Determine new alpha and beta based on new mu and sigma for plotting.
post.alpha =  alpha + y  
post.beta  = beta + n - y 

## Plot posterior first b/c of the y limits
x = seq(0, 1, by=0.01)
df = data.frame(x = x, 
                y1 = dbeta(x = x,
                           shape1 = alpha, 
                           shape2 = beta),
                y2 = dbeta(x = seq(0, 1, by=0.01), 
                          shape1 = post.alpha, 
                          shape2 = post.beta))

ggplot(df, aes(x = x)) + 
  geom_line(aes(y = y1)) +                        ## prior
  geom_line(aes(y = y2), color = 'blue') +        ## posterior
  geom_vline(xintercept = post.mu, color = 'red') ## posterior mean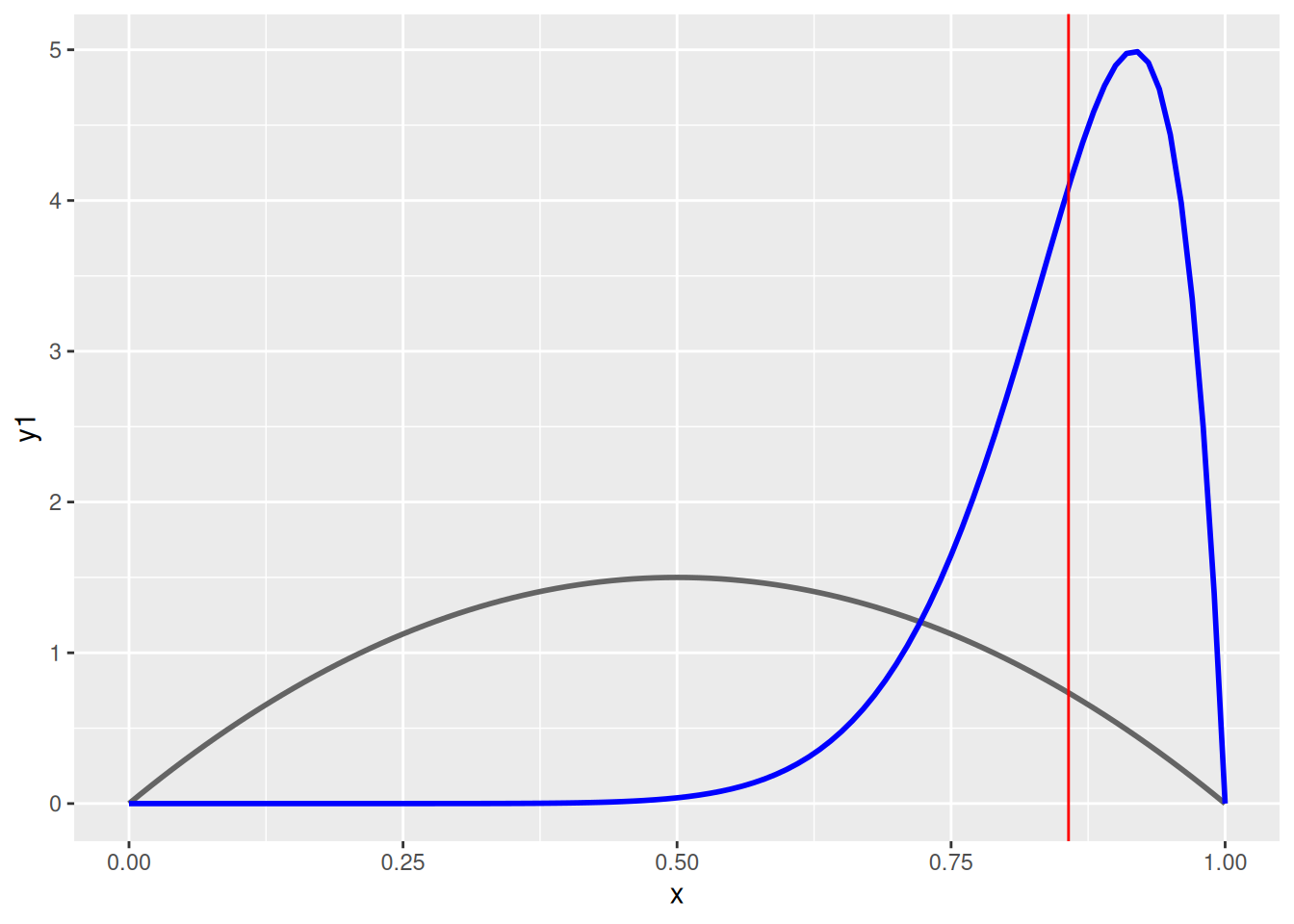

Code 
post.mu
[1] 0.8571429

You can choose alpha and beta using the mean and variance of your data (https://en.wikipedia.org/wiki/Beta_distribution#Mean_and_variance).

Code 
## Compute mean and variance from data 
mu = .5
sigma2 = 0.05

## Find the alpha and beta for the corresponding Beta distribution
nu    = mu*(1-mu)/sigma2 - 1
alpha =    mu * nu
beta  = (1-mu)* nu
alpha
beta
[1] 2
[1] 2